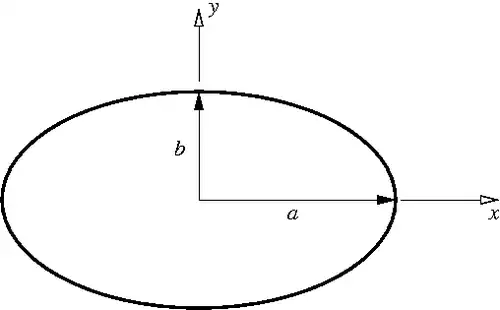
Solution
The Prandtl stress function must satisfy the compatibility condition

Plugging in the stress function, we have,
![{\displaystyle C\left[{\frac {2}{a^{2}}}+{\frac {2}{b^{2}}}\right]=-2\mu \alpha }](../8f4106623b3d06e4e35ff26b822ff225e3546d18.svg)
or,

The torque for a simply connected section is given by

For the elliptical cross-section, we have
![{\displaystyle {\begin{aligned}T&=2\int _{-a}^{a}\left[\int _{-b{\sqrt {(1-x^{2}/a^{2})}}}^{b{\sqrt {(1-x^{2}/a^{2})}}}C\left({\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-1\right)~dy\right]~dx\\&=2C\int _{-a}^{a}\left[\left|{\frac {x^{2}~y}{a^{2}}}+{\frac {y^{3}}{3b^{2}}}-y\right|_{-b{\sqrt {(1-x^{2}/a^{2})}}}^{b{\sqrt {(1-x^{2}/a^{2})}}}\right]~dx\\&=2C\int _{-a}^{a}\left[\left|y\left[{\frac {y^{2}}{3b^{2}}}-\left(1-{\frac {x^{2}}{a^{2}}}\right)\right]\right|_{-b{\sqrt {(1-x^{2}/a^{2})}}}^{b{\sqrt {(1-x^{2}/a^{2})}}}\right]~dx\\&=2C\int _{-a}^{a}2b\left({\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)\left[{\frac {1}{3}}\left(1-{\frac {x^{2}}{a^{2}}}\right)-\left(1-{\frac {x^{2}}{a^{2}}}\right)\right]~dx\\&=-{\frac {8bC}{3}}\int _{-a}^{a}\left[\left(1-{\frac {x^{2}}{a^{2}}}\right)^{(3/2)}\right]~dx=-{\frac {8bC}{3a^{3}}}\int _{-a}^{a}\left[\left(a^{2}-x^{2}\right)^{(3/2)}\right]~dx\\&=-{\frac {8bC}{3a^{3}}}\left[(2){\frac {(1)(3)}{(2)(4)}}{\frac {\pi }{2}}a^{4}\right]=-\pi ~a~b~C\end{aligned}}}](../50a60e627697c2033a6b92756ea41c208d46efba.svg)
Therefore,

or,

The torsion constant  is given by
is given by

The stresses in the section are given by

The projected shear traction is

The maximum projected shear traction is at  . Hence,
. Hence,

To express the magnitude of the maximum shear stress in terms
of  ,
,  , and
, and  , we use
, we use

Therefore,