Elasticity/Sample final 3

Consider the curved beam ${\displaystyle a<r<b}$ and ${\displaystyle 0<\theta <\alpha }$, loaded by a bending moment ${\displaystyle M_{0}}$ (but no forces) shown in the figure below.

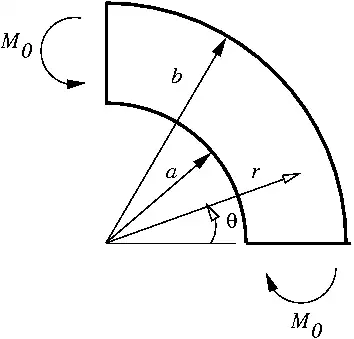
• (a) Using equilibrium and symmetry considerations, write down a stress function for this problem by choosing the appropriate terms from Michell's solution.
• (b) Find the stress components that correspond to the stress function you have chosen (you do not have to evaluate the constants).
• (c) Write down the strong form of the boundary conditions for this problem in terms of components of the stress tensor. (You can use your own symbols to represent surface traction distributions that you cannot specify explicitly).
• (d) Which strong boundary conditions would you have to substitute with weak boundary conditions (in the St. Venant sense) in order to solve this problem. Write down the appropriate weak boundary conditions in terms of components of the stress tensor.

Consider the equilibrium of a small section of the beam (free-body diagram). It is obvious that any such section will look exactly like the diagram of the whole beam. Thus, the stresses in the beam cannot vary with ${\displaystyle \theta }$ and the beam must be axisymmetric.

Therefore, the appropriate stress function for this problem is (from Michell's solution)

${\displaystyle {\varphi =A~r^{2}+B~r^{2}~\ln(r)+C~\ln(r)+D\theta }}$

The stress components corresponding to this stress function are

${\displaystyle {\sigma _{rr}=2A+2B\ln(r)+B+{\frac {C}{r^{2}}}}}$

${\displaystyle {\sigma _{\theta \theta }=2A+2B\ln(r)+3B-{\frac {C}{r^{2}}}}}$

${\displaystyle {\sigma _{r\theta }={\frac {D}{r^{2}}}}}$

At ${\displaystyle r=a}$, ${\displaystyle {\widehat {\mathbf {n} }}{}=-{\widehat {\mathbf {e} }}_{r}=(-1,0)}$ and ${\displaystyle \mathbf {t} =(0,0)}$.\

Therefore,

${\displaystyle t_{i}=n_{j}\sigma _{ij}~~\Rightarrow ~~t_{r}=n_{r}\sigma _{rr}+n_{\theta }\sigma _{r\theta }~~\Rightarrow \sigma _{rr}=0~~{\text{and}}~~t_{\theta }=n_{r}\sigma _{\theta r}+n_{\theta }\sigma _{\theta \theta }~~\Rightarrow \sigma _{r\theta }=0}$

At ${\displaystyle r=b}$, ${\displaystyle {\widehat {\mathbf {n} }}{}={\widehat {\mathbf {e} }}_{r}=(1,0)}$ and ${\displaystyle \mathbf {t} =(0,0)}$.

Therefore,

${\displaystyle t_{i}=n_{j}\sigma _{ij}~~\Rightarrow ~~t_{r}=n_{r}\sigma _{rr}+n_{\theta }\sigma _{r\theta }~~\Rightarrow \sigma _{rr}=0~~{\text{and}}~~t_{\theta }=n_{r}\sigma _{\theta r}+n_{\theta }\sigma _{\theta \theta }~~\Rightarrow \sigma _{r\theta }=0}$

At ${\displaystyle \theta =0}$, ${\displaystyle {\widehat {\mathbf {n} }}{}=-{\widehat {\mathbf {e} }}_{\theta }=(0,-1)}$ and ${\displaystyle \mathbf {t} =(-T_{r}(r),-T_{\theta }(r))}$, where ${\displaystyle T_{r}}$ and ${\displaystyle T_{\theta }}$ are unknown traction distributions that correspond to the applied moments.

Therefore,

${\displaystyle t_{i}=n_{j}\sigma _{ij}~~\Rightarrow ~~t_{r}=n_{r}\sigma _{rr}+n_{\theta }\sigma _{r\theta }~~\Rightarrow \sigma _{r\theta }=T_{r}(r)~~{\text{and}}~~t_{\theta }=n_{r}\sigma _{\theta r}+n_{\theta }\sigma _{\theta \theta }~~\Rightarrow \sigma _{\theta \theta }=T_{\theta }(r)}$

At ${\displaystyle \theta =\alpha }$, ${\displaystyle {\widehat {\mathbf {n} }}{}={\widehat {\mathbf {e} }}_{\theta }=(0,1)}$ and ${\displaystyle \mathbf {t} =(T_{r}(r),T_{\theta }(r))}$.

${\displaystyle t_{i}=n_{j}\sigma _{ij}~~\Rightarrow ~~t_{r}=n_{r}\sigma _{rr}+n_{\theta }\sigma _{r\theta }~~\Rightarrow \sigma _{r\theta }=T_{r}(r)~~{\text{and}}~~t_{\theta }=n_{r}\sigma _{\theta r}+n_{\theta }\sigma _{\theta \theta }~~\Rightarrow \sigma _{\theta \theta }=T_{\theta }(r)}$

Therefore, the strong boundary conditions for this problem are

${\displaystyle {{\text{at}}~r=a~{\text{and}}~r=b~~;~~\sigma _{rr}=0~{\text{and}}~\sigma _{r\theta }=0}}$

${\displaystyle {{\text{at}}~\theta =0~{\text{and}}~\theta =\alpha ~~;~~\sigma _{r\theta }=T_{r}(r)~{\text{and}}~\sigma _{\theta \theta }=T_{\theta }(r)}}$

In setting up the weak forms of the boundary conditions, we have to set the average tractions over the boundaries ${\displaystyle \theta =0}$ and ${\displaystyle \theta =\alpha }$ to zero and the moment due to the traction distribution to ${\displaystyle M_{0}}$, i.e.,

${\displaystyle \int _{a}^{b}T_{r}(r)~dr=0~~;~~\int _{a}^{b}T_{\theta }(r)~dr=0~~;~~\int _{a}^{b}T_{\theta }(r)~r~dr=M_{0}}$

The traction ${\displaystyle T_{r}(r)}$ acts in the direction of ${\displaystyle r}$ and goes not generate any moments.

Therefore, the weak forms of the traction BCs are

${\displaystyle {{\text{at}}~\theta =0~{\text{and}}~\theta =\alpha ~~;~~\int _{a}^{b}\sigma _{r\theta }~dr=0~~;~~\int _{a}^{b}\sigma _{\theta \theta }~dr=0~~{\text{and}}\int _{a}^{b}\sigma _{\theta \theta }~r~dr=M_{0}}}$