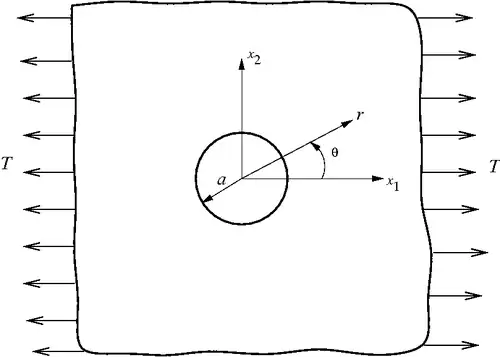
Consider the elastic plate with a hole subject to uniaxial tension.
Solution
We can use the following Maple code to show the above results.
phi := T*r^2/4*(1 - cos(2*theta)) + A*ln(r) + B*theta + C*cos(2*theta) +
D/r^2*cos(2*theta);
srr := 1/r*diff(phi,r) + 1/r^2*diff(phi,theta,theta);
stt := diff(phi,r,r);
srt := -diff((1/r*diff(phi,theta)),r);
srra := collect(simplify(eval(srr, r=a)),{cos});
srta := collect(simplify(eval(srt, r=a)),{cos});
eq1 := coeff(srra, cos(2*theta));
eq2 := coeff(srta, sin(2*theta));
eq3 := 1/2*(T*a^4+2*A*a^2)/a^4;
eq4 := 1/a^2*B;
BB := solve({eq4=0},{B});
AA := solve({eq3=0},{A});
sol := solve({eq1=0,eq2=0},{C,D});
phi := subs(BB, phi);
phi := subs(AA, phi);
phi := subs(sol, phi);
srr2 := 1/r*diff(phi,r) + 1/r^2*diff(phi,theta,theta);
stt2 := diff(phi,r,r);
srt2 := -diff((1/r*diff(phi,theta)),r);
srr3 := collect(simplify(srr2),{cos});
stt3 := collect(simplify(stt2),{cos});
srt3 := collect(simplify(srt2),{cos});
The stresses at the hole (
r
=
a
{\displaystyle r=a}
σ
r
r
=
0
σ
θ
θ
=
T
−
2
T
cos
(
2
θ
)
σ
r
θ
=
0
{\displaystyle {\begin{aligned}\sigma _{rr}&=0\\\sigma _{\theta \theta }&=T-2T\cos(2\theta )\\\sigma _{r\theta }&=0\end{aligned}}}
The maximum hoop stress is given at
θ
=
0
{\displaystyle \theta =0}
θ
=
π
/
2
{\displaystyle \theta =\pi /2}
At
θ
=
0
{\displaystyle \theta =0}
σ
θ
θ
=
−
T
{\displaystyle \sigma _{\theta \theta }=-T}
At
θ
=
π
/
2
{\displaystyle \theta =\pi /2}
σ
θ
θ
=
3
T
{\displaystyle \sigma _{\theta \theta }=3T}
The maximum shear stress at
r
=
a
{\displaystyle r=a}
τ
max
=
1.5
T
{\displaystyle \tau _{\text{max}}=1.5T}
r
=
∞
{\displaystyle r=\infty }
0.5
T
{\displaystyle 0.5T}
Therefore, the stress concentration factor in tension is
3
T
/
T
=
3
{\displaystyle 3T/T=3}
1.5
T
/
0.5
T
=
3
{\displaystyle 1.5T/0.5T=3}
Both stress concentration factors are equal.
θ
=
π
/
2
{\displaystyle \theta =\pi /2}
σ
θ
θ
=
T
/
2
(
1
−
cos
2
θ
)
{\displaystyle \sigma _{\theta \theta }=T/2(1-\cos 2\theta )}
The ratio is
ratio
=
1
+
3
a
4
2
r
4
+
a
2
2
r
2
{\displaystyle {\text{ratio}}=1+{\frac {3a^{4}}{2r^{4}}}+{\frac {a^{2}}{2r^{2}}}}
This ratio is 0.95 when
r
≈
3.5
a
{\displaystyle r\approx 3.5a}
1.75
{\displaystyle 1.75}
φ
=
T
r
2
4
−
T
r
2
cos
(
2
θ
)
4
+
A
ln
(
r
)
+
B
θ
+
C
cos
(
2
θ
)
+
D
r
−
2
cos
(
2
θ
)
{\displaystyle \varphi ={\frac {Tr^{2}}{4}}-{\frac {Tr^{2}\cos(2\theta )}{4}}+A\ln(r)+B\theta +C\cos(2\theta )+Dr^{-2}\cos(2\theta )}
Therefore, the displacement field from the Michell solution is
2
μ
u
r
=
T
4
[
(
κ
−
1
)
r
]
−
T
4
[
−
2
r
cos
(
2
θ
)
]
+
A
[
−
1
r
]
+
C
[
(
κ
+
1
)
r
−
1
cos
(
2
θ
)
]
+
D
[
2
r
−
3
cos
(
2
θ
)
]
2
μ
u
θ
=
−
T
4
[
2
r
sin
(
2
θ
)
]
+
C
[
−
(
κ
−
1
)
r
−
1
sin
(
2
θ
)
]
+
D
[
2
r
−
3
sin
(
2
θ
)
]
{\displaystyle {\begin{aligned}2\mu u_{r}&={\frac {T}{4}}\left[(\kappa -1)r\right]-{\frac {T}{4}}\left[-2r\cos(2\theta )\right]+A\left[-{\frac {1}{r}}\right]+C\left[(\kappa +1)r^{-1}\cos(2\theta )\right]+D\left[2r^{-3}\cos(2\theta )\right]\\2\mu u_{\theta }&=-{\frac {T}{4}}\left[2r\sin(2\theta )\right]+C\left[-(\kappa -1)r^{-1}\sin(2\theta )\right]+D\left[2r^{-3}\sin(2\theta )\right]\end{aligned}}}
From the stress calculation step, we have
A
=
−
T
a
2
2
;
B
=
0
;
C
=
T
a
2
2
;
D
=
−
T
a
4
4
{\displaystyle A=-{\frac {Ta^{2}}{2}}~;~~B=0~;~~C={\frac {Ta^{2}}{2}}~;~~D=-{\frac {Ta^{4}}{4}}}
After substituting the constants and collecting terms,
2
μ
u
r
=
T
r
cos
(
2
θ
)
2
[
1
+
(
κ
+
1
)
a
2
r
2
−
a
4
r
4
]
+
T
r
4
[
(
κ
−
1
)
+
2
a
2
r
2
]
2
μ
u
θ
=
−
T
r
sin
(
2
θ
)
2
[
1
+
(
κ
−
1
)
a
2
r
2
+
a
4
r
4
]
{\displaystyle {\begin{aligned}2\mu u_{r}&={\frac {Tr\cos(2\theta )}{2}}\left[1+(\kappa +1){\frac {a^{2}}{r^{2}}}-{\frac {a^{4}}{r^{4}}}\right]+{\frac {Tr}{4}}\left[(\kappa -1)+2{\frac {a^{2}}{r^{2}}}\right]\\2\mu u_{\theta }&=-{\frac {Tr\sin(2\theta )}{2}}\left[1+(\kappa -1){\frac {a^{2}}{r^{2}}}+{\frac {a^{4}}{r^{4}}}\right]\end{aligned}}}
Replacing
μ
{\displaystyle \mu }
E
2
(
1
+
ν
)
{\displaystyle {\frac {E}{2(1+\nu )}}}
κ
{\displaystyle \kappa }
3
−
ν
1
+
ν
{\displaystyle {\frac {3-\nu }{1+\nu }}}
u
r
=
T
r
cos
(
2
θ
)
2
E
[
(
1
+
ν
)
+
4
a
2
r
2
−
(
1
+
ν
)
a
4
r
4
]
+
T
r
2
E
[
(
1
−
ν
)
+
(
1
+
ν
)
a
2
r
2
]
u
θ
=
−
T
r
sin
(
2
θ
)
2
E
[
(
1
+
ν
)
+
2
(
1
−
ν
)
a
2
r
2
+
(
1
+
ν
)
a
4
r
4
]
{\displaystyle {\begin{aligned}u_{r}&={\frac {Tr\cos(2\theta )}{2E}}\left[(1+\nu )+4{\frac {a^{2}}{r^{2}}}-(1+\nu ){\frac {a^{4}}{r^{4}}}\right]+{\frac {Tr}{2E}}\left[(1-\nu )+(1+\nu ){\frac {a^{2}}{r^{2}}}\right]\\u_{\theta }&=-{\frac {Tr\sin(2\theta )}{2E}}\left[(1+\nu )+2(1-\nu ){\frac {a^{2}}{r^{2}}}+(1+\nu ){\frac {a^{4}}{r^{4}}}\right]\end{aligned}}}
At
r
=
a
{\displaystyle r=a}
u
r
=
T
a
E
[
1
+
2
cos
(
2
θ
)
]
u
θ
=
−
2
T
a
E
sin
(
2
θ
)
{\displaystyle {\begin{aligned}u_{r}&={\frac {Ta}{E}}\left[1+2\cos(2\theta )\right]\\u_{\theta }&=-{\frac {2Ta}{E}}\sin(2\theta )\end{aligned}}}
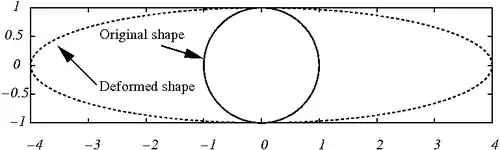
The deformed shape is shown below:
Deformation of the hole under tension
In cartesian coordinates, the displacement field is given by
u
x
(
r
,
θ
)
=
T
a
8
μ
[
r
a
(
κ
+
1
)
cos
θ
+
2
a
r
(
(
1
+
κ
)
cos
θ
+
cos
3
θ
)
−
2
a
3
r
3
cos
3
θ
]
,
u
y
(
r
,
θ
)
=
T
a
8
μ
[
r
a
(
κ
−
3
)
sin
θ
+
2
a
r
(
(
1
−
κ
)
sin
θ
+
sin
3
θ
)
−
2
a
3
r
3
sin
3
θ
]
{\displaystyle {\begin{aligned}u_{x}(r,\theta )&=&{\frac {Ta}{8\mu }}\left[{\frac {r}{a}}(\kappa +1)\cos \theta +{\frac {2a}{r}}((1+\kappa )\cos \theta +\cos 3\theta )-{\frac {2a^{3}}{r^{3}}}\cos 3\theta \right],\\u_{y}(r,\theta )&=&{\frac {Ta}{8\mu }}\left[{\frac {r}{a}}(\kappa -3)\sin \theta +{\frac {2a}{r}}((1-\kappa )\sin \theta +\sin 3\theta )-{\frac {2a^{3}}{r^{3}}}\sin 3\theta \right]\end{aligned}}}