Elasticity/Energy methods example 4

< Elasticity

Example 4 : Bending of a cantilevered beam

Bending of a cantilevered beam

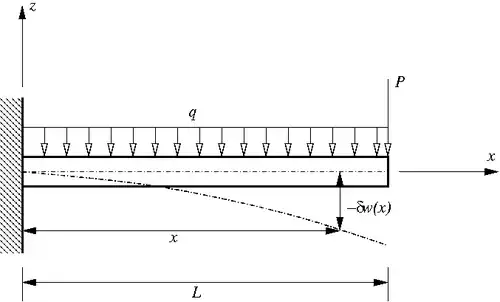
Application of the Principle of Virtual Work

The virtual work done by the external applied forces in moving through the virtual displacement $\delta w(x)\,$ is given by

\delta W_{\text{ext}}=\int _{0}^{L}q~\delta w~dx+P~\delta w(L)

The work done by the internal forces are,

{\begin{aligned}\delta W_{\text{int}}&=\int _{\mathcal {R}}\delta U~dV\\&=\int _{0}^{L}\int _{\mathcal {S}}\delta \left({\frac {1}{2}}\sigma _{ij}\varepsilon _{ij}\right)~dA~dx\\&=\int _{0}^{L}\int _{\mathcal {S}}\sigma _{ij}\delta \varepsilon _{ij}~dA~dx\end{aligned}}

From beam theory, the displacement field at a point in the beam is given by

u=-z{\frac {dw}{dx}}~~;~~v=0~~;~~w=w(x)

The strains are, neglecting Poisson effects,

\varepsilon _{xx}={\frac {\partial u}{\partial x}}=-z{\frac {d^{2}w}{dx^{2}}}~~;~~\varepsilon _{yy}=0~~;~~\varepsilon _{zz}=0

and the corresponding stresses are

\sigma _{xx}=E\varepsilon _{xx}=-Ez{\frac {d^{2}w}{dx^{2}}}~~;~~\sigma _{yy}=0~~;~~\sigma _{zz}=0

If we also neglect the shear strains and stresses, we get

{\begin{aligned}\delta W_{\text{int}}=&=\int _{0}^{L}\int _{\mathcal {S}}\sigma _{xx}\delta \varepsilon _{xx}~dA~dx\\&=\int _{0}^{L}\int _{\mathcal {S}}E~\varepsilon _{xx}\delta \varepsilon _{xx}~dA~dx\\&=\int _{0}^{L}E{\frac {d^{2}w}{dx^{2}}}{\frac {d^{2}(\delta w)}{dx^{2}}}\left(\int _{\mathcal {S}}z^{2}~dA\right)~dx\\&=\int _{0}^{L}E~I{\frac {d^{2}w}{dx^{2}}}{\frac {d^{2}(\delta w)}{dx^{2}}}dx\end{aligned}}

Therefore, from the principle of virtual work,

\delta W=\int _{0}^{L}\left(E~I{\frac {d^{2}w}{dx^{2}}}{\frac {d^{2}(\delta w)}{dx^{2}}}+q~\delta w\right)~dx+P~\delta w(L)=0

Integrating by parts and after some manipulation, we get,

{\begin{aligned}0&=\int _{0}^{L}\left[{\frac {d^{2}}{dx^{2}}}\left(E~I{\frac {d^{2}w}{dx^{2}}}\right)+q+P\delta (L-x)\right]\delta w~dx+\left.\left[\left(E~I{\frac {d^{2}w}{dx^{2}}}\right)\delta \left({\frac {dw}{dx}}\right)+{\frac {d}{dx}}\left(E~I{\frac {d^{2}w}{dx^{2}}}\right)\delta w\right]\right|_{0}^{L}\end{aligned}}

where $\delta (L-x)$ is the Dirac delta function,

\int _{-\infty }^{\infty }\delta (L-x)~f(x)~dx=f(L)

The Euler equation for the beam is, therefore,

{\frac {d^{2}}{dx^{2}}}\left(E~I{\frac {d^{2}w}{dx^{2}}}\right)+q+P\delta (L-x)=0

and the boundary conditions are

{\begin{aligned}E~I{\frac {d^{2}w}{dx^{2}}}(L)&=0\\\left.{\frac {d}{dx}}\left(E~I{\frac {d^{2}w}{dx^{2}}}\right)\right|_{x=L}&=0\end{aligned}}

Application of the Hellinger-Prange-Reissner variational principle

The governing equations of the cantilever beam can be written as

Kinematics

\kappa ={\frac {d^{2}w}{dx^{2}}}~~;~~w(0)=0~~;~~\left.{\frac {dw}{dx}}\right|_{x=0}=0

Constitutive Equation

M=EI\kappa

Equilibrium (kinetics)

{\frac {d^{2}M}{dx^{2}}}+q+P\delta (L-x)=0~~;~~M(L)=0~~;~~\left.{\frac {dM}{dx}}\right|_{x=L}=0

Recall that the Hellinger-Prange-Reissner functional is given by

{\mathcal {H}}[s]=\int _{\mathcal {B}}U^{c}({\boldsymbol {\sigma }})-\int _{\mathcal {B}}{\boldsymbol {\sigma }}:{\boldsymbol {\varepsilon }}~dV-\int _{\mathcal {B}}\mathbf {f} \bullet \mathbf {u} ~dV+\int _{\partial {\mathcal {B}}^{u}}\mathbf {t} \bullet (\mathbf {u} -{\widehat {\mathbf {u} }})~dA+\int _{\partial {\mathcal {B}}^{t}}{\widehat {\mathbf {t} }}\bullet \mathbf {u} ~dA

If we apply the strain-displacement constraints using the Lagrange multipliers ${\boldsymbol {\lambda }}\,$ and the displacement boundary conditions using the Lagrange multipliers ${\boldsymbol {\mu }}\,$ , we get a modified functional

{\bar {\mathcal {H}}}[\mathbf {u} ,{\boldsymbol {\varepsilon }},{\boldsymbol {\lambda }},{\boldsymbol {\mu }}]=\int _{\mathcal {B}}\left[U({\boldsymbol {\varepsilon }})+{\boldsymbol {\lambda }}:[{\frac {1}{2}}({\boldsymbol {\nabla }}\mathbf {u} -{\boldsymbol {\nabla }}\mathbf {u} ^{T})-{\boldsymbol {\varepsilon }}]-\mathbf {f} \bullet \mathbf {u} \right]~dV-\int _{\partial {\mathcal {B}}^{u}}{\boldsymbol {\mu }}\bullet (\mathbf {u} -{\widehat {\mathbf {u} }})~dA-\int _{\partial {\mathcal {B}}^{t}}{\widehat {\mathbf {t} }}\bullet \mathbf {u} ~dA

For the cantilevered beam, the above functional becomes

{\begin{aligned}{\bar {\mathcal {H}}}[w,\kappa ,\lambda ,\mu _{1},\mu _{2}]=&\int _{0}^{L}\left[{\frac {EI}{2}}\kappa ^{2}+\left({\frac {d^{2}w}{dx^{2}}}-\kappa \right)\lambda +[q+P\delta (L-x)]~w\right]~dx\\&-M(L){\frac {dw}{dx}}(L)-{\frac {dM}{dx}}(L)~w(L)+\mu _{1}[w(0)-0]+\mu _{2}[{\frac {dw}{dx}}(0)-0]\end{aligned}}

Taking the first variation of the functional, we can easily derive the Euler equations and the associated BCs.

{\displaystyle {\begin{aligned}\delta \kappa

and

{\begin{aligned}{\frac {d}{dx}}(\delta w):~~~&\lambda (0)=\mu _{2}~~,~~\lambda (L)=M(L)\\\delta w:~~~&{\frac {d\lambda }{dx}}(0)=-\mu _{1}~~,~~{\frac {d\lambda }{dx}}(L)={\frac {dM}{dx}}(L)\\\delta \mu _{1}:~~~&w(0)=0\\\delta \mu _{1}:~~~&{\frac {dw}{dx}}(0)=0\end{aligned}}

The same process can be used to derive Euler equations using the Hu-Washizu variational principle.