Elasticity/Antiplane shear example 1

Given:

The body ${\displaystyle -\alpha <\theta <\alpha }$, ${\displaystyle 0\leq r<a}$ is supported at ${\displaystyle r=a}$ and loaded only by a uniform antiplane shear traction ${\displaystyle \sigma _{\theta z}=S}$ on the surface ${\displaystyle \theta =\alpha }$, the other surface being traction-free.

Find:

Find the complete stress field in the body, using strong boundary conditions on ${\displaystyle \theta =\pm \alpha }$ and weak conditions on ${\displaystyle r=a}$.

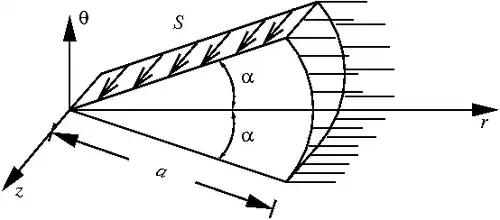
[Hint: Since the traction ${\displaystyle \sigma _{\theta z}}$ is uniform on the surface ${\displaystyle \theta =\alpha }$, from the expression for antiplane stress we can see that the displacement varies with ${\displaystyle r^{1}=r}$. The most general solution for the equilibrium equation for this behavior is ${\displaystyle u(r,\theta )=Ar\cos \theta +Br\sin \theta }$]

Step 1: Identify boundary conditions

${\displaystyle {\begin{aligned}{\text{at}}~r&=0~;~~u_{r}=0,u_{\theta }=0\\{\text{at}}~r&=a~;~~u_{r}=0,u_{\theta }=0,u_{z}=0\\{\text{at}}~\theta &=-\alpha ~;~~t_{\theta }=0,t_{r}=0,t_{z}=0\\{\text{at}}~\theta &=\alpha ~;~~t_{\theta }=0,t_{r}=0,t_{z}=S\end{aligned}}}$

The traction boundary conditions in terms of components of the stress tensor are

${\displaystyle {\begin{aligned}{\text{at}}~\theta &=-\alpha ~;~~\sigma _{\theta r}=0,\sigma _{\theta \theta }=0,\sigma _{\theta z}=0\\{\text{at}}~\theta &=\alpha ~;~~\sigma _{\theta r}=0,\sigma _{\theta \theta }=0,\sigma _{\theta z}=S\end{aligned}}}$

Step 2: Assume solution

Assume that the problem satisfies the conditions required for antiplane shear. If ${\displaystyle \sigma _{\theta z}}$ is to be uniform along ${\displaystyle \theta =\alpha }$, then

${\displaystyle \sigma _{\theta z}={\frac {\mu }{r}}{\frac {\partial u_{z}}{\partial \theta }}=C}$

or,

${\displaystyle {\frac {\partial u_{z}}{\partial \theta }}={\frac {Cr}{\mu }}}$

The general form of ${\displaystyle u_{z}}$ that satisfies the above requirement is

${\displaystyle u_{z}(r,\theta )=Ar\cos \theta +Br\sin \theta +C}$

where ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ are constants.

Step 3: Compute stresses

The stresses are

${\displaystyle {\begin{aligned}\sigma _{\theta z}&={\frac {\mu }{r}}{\frac {\partial u_{z}}{\partial \theta }}=\mu \left(-A\sin \theta +B\cos \theta \right)\\\sigma _{rz}&=\mu {\frac {\partial u_{z}}{\partial r}}=\mu \left(A\cos \theta +B\sin \theta \right)\end{aligned}}}$

Step 4: Check if traction BCs are satisfied

The antiplane strain assumption leads to the ${\displaystyle \sigma _{\theta \theta }}$ and ${\displaystyle \sigma _{r\theta }}$ BCs being satisfied. From the boundary conditions on ${\displaystyle \sigma _{\theta z}}$, we have

${\displaystyle {\begin{aligned}0&=\mu \left(A\sin \alpha +B\cos \alpha \right)\\S&=\mu \left(-A\sin \alpha +B\cos \alpha \right)\end{aligned}}}$

Solving,

${\displaystyle A=-{\frac {S}{2\mu \sin \alpha }}~;~~B={\frac {S}{2\mu \cos \alpha }}}$

This gives us the stress field

${\displaystyle \sigma _{\theta z}={\frac {S}{2}}\left({\frac {\sin \theta }{\sin \alpha }}+{\frac {\cos \theta }{\cos \alpha }}\right)~;~~\sigma _{rz}={\frac {S}{2}}\left(-{\frac {\cos \theta }{\sin \alpha }}+{\frac {\sin \theta }{\cos \alpha }}\right)}$

Step 5: Compute displacements

The displacement field is

${\displaystyle u_{z}(r,\theta )={\frac {Sr}{2\mu }}\left(-{\frac {\cos \theta }{\sin \alpha }}+{\frac {\sin \theta }{\cos \alpha }}\right)+C}$

where the constant ${\displaystyle C}$ corresponds to a superposed rigid body displacement.

Step 6: Check if displacement BCs are satisfied

The displacement BCs on ${\displaystyle u_{r}}$ and ${\displaystyle u_{\theta }}$ are automatically satisfied by the antiplane strain assumption. We will try to satisfy the boundary conditions on ${\displaystyle u_{z}}$ in a weak sense, i.e, at ${\displaystyle r=a}$,

${\displaystyle \int _{-\alpha }^{\alpha }u_{z}(a,\theta )d\theta =0~.}$

This weak condition does not affect the stress field. Plugging in ${\displaystyle u_{z}}$,

${\displaystyle {\begin{aligned}0&=\int _{-\alpha }^{\alpha }u_{z}(a,\theta )d\theta \\&={\frac {Sa}{2\mu }}\int _{-\alpha }^{\alpha }\left(-{\frac {\cos \theta }{\sin \alpha }}+{\frac {\sin \theta }{\cos \alpha }}+C{\frac {2\mu }{Sa}}\right)d\theta \\&={\frac {Sa}{2\mu }}\int _{-\alpha }^{\alpha }\left(-{\frac {\cos \theta }{\sin \alpha }}+{\frac {\sin \theta }{\cos \alpha }}+C{\frac {2\mu }{Sa}}\right)d\theta \\&={\frac {Sa}{2\mu }}\left[\left(-{\frac {\sin \theta }{\sin \alpha }}-{\frac {\cos \theta }{\cos \alpha }}+C\theta {\frac {2\mu }{Sa}}\right)\right]_{-\alpha }^{\alpha }\\&={\frac {Sa}{2\mu }}\left(-2{\frac {\sin \alpha }{\sin \alpha }}+2C\alpha {\frac {2\mu }{Sa}}\right)\\&=-{\frac {Sa}{\mu }}+C\alpha \end{aligned}}}$

Therefore,

${\displaystyle C={\frac {Sa}{2\mu \alpha }}}$

The approximate displacement field is

${\displaystyle u_{z}(r,\theta )={\frac {S}{2\mu }}\left(-r{\frac {\cos \theta }{\sin \alpha }}+r{\frac {\sin \theta }{\cos \alpha }}+a{\frac {1}{\alpha }}\right)}$