Elasticity/Torsion of circular cylinders
< Elasticity
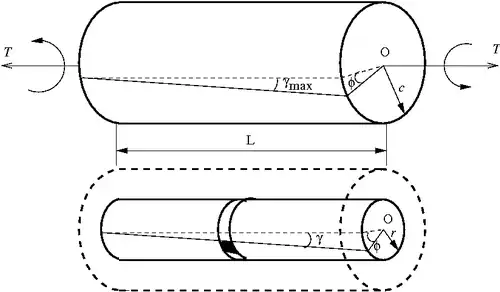
Torsion of Circular Cylinders
 |
About the problem:
- Circular Cylinder.
- Centroidal axis thru the center of each cross section (c.s.)
- Length , Outer radius .
- Applied torque .
- Angle of twist .
Assumptions:
- Each c.s. remains plane and undistorted.
- Each c.s. rotates through the same angle.
- No warping or change in shape.
- Amount of displacement of each c.s. is proportional to distance from end.
Find:
- Shear strains in the cylinder ().
- Shear stress in the cylinder ().
- Relation between torque () and angle of twist ().
- Relation between torque () and shear stress ().
Solution:
If is small, then
Therefore,
If the material is linearly elastic,
Therefore,
The torque on each c.s. is given by
where is the polar moment of inertia of the c.s.
Therefore,
and