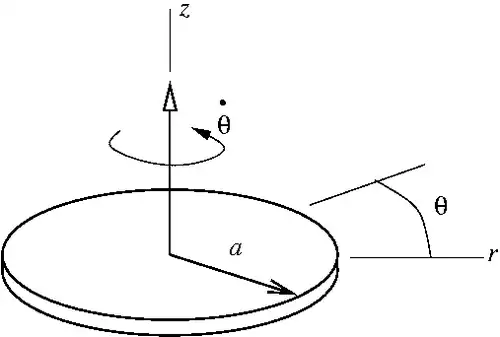
Solution:
The acceleration of a point ( ) on the disk is
) on the disk is

The body force field is

Since there is no rotational acceleration, the body force can be
derived from a potential  . The relations between the stresses, the Airy stress function and the body force potential are
. The relations between the stresses, the Airy stress function and the body force potential are

where

From equations (2) and (6) , we have,

Integrating equation (7), we have

Substituting equation (9) into equation (8), we get

This constant can be set to zero without loss of generality. Therefore,

The spinning disk problem is a plane stress problem. Hence the compatibility
condition is

where
![{\displaystyle {\begin{aligned}{\text{(13)}}\qquad \nabla ^{2}{()}&={\frac {\partial ^{2}()}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial ()}{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}()}{\partial \theta }}\\{\text{(14)}}\qquad \nabla ^{4}{()}&=\nabla ^{2}{[\nabla ^{2}{()}]}\end{aligned}}}](../b7c4b6898d9dcbd10774b5fce37a6bcd844aa613.svg)
Now, from equations (11) and (13)
![{\displaystyle {\text{(15)}}\qquad \nabla ^{2}{V}=-\rho {\dot {\theta }}^{2}[1+1+0]=-2\rho {\dot {\theta }}^{2}}](../7ac9f17a00a009a0658769d5a31a1d0317416673.svg)
Therefore, equation (12) becomes

Since the problem is axisymmetric, there can be no shear stresses, i.e.  and no dependence on
and no dependence on  . From Michell's solution, the appropriate terms of the Airy stress function are
. From Michell's solution, the appropriate terms of the Airy stress function are

Axisymmetry also requires that  , the displacement in the
, the displacement in the  direction must be zero. However, if we look at Mitchell's solution, we see that
direction must be zero. However, if we look at Mitchell's solution, we see that  is non-zero if the term
is non-zero if the term
 is used in the Airy stress function. Hence, we reject this term and are left with
is used in the Airy stress function. Hence, we reject this term and are left with

If we plug this stress function into equation (16) we see that
 . Therefore, equation (18) represents a homogeneous solution of equation (16). The
. Therefore, equation (18) represents a homogeneous solution of equation (16). The  that is a general solution of equation (16) is obtained by adding a particular solution of the equation.
that is a general solution of equation (16) is obtained by adding a particular solution of the equation.
One such particular solution is the stress function  since the biharmonic equation must evaluate to a constant. Plugging this into equation (16) we have
since the biharmonic equation must evaluate to a constant. Plugging this into equation (16) we have

or,

Therefore, the general solution is

The corresponding stresses are (from equations (3, 4, 5)),

At  , the stresses must be finite. Hence,
, the stresses must be finite. Hence,  . At
. At  ,
,  . Evaluating
. Evaluating  at
at  we get
we get

Substituting back into equations (22) and (23), we get

![{\displaystyle {\text{(27)}}\qquad \sigma _{\theta \theta }={\frac {\rho {\dot {\theta }}^{2}}{8}}\left[(3+\nu )a^{2}-(1+3\nu )r^{2}\right]}](../de47f3f43c93ff4521d61304a97c3e900faf9ac5.svg)