Strain Measures in three dimensions
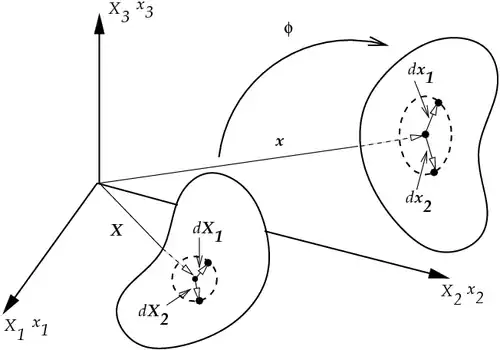 The motion of a body The motion of a body |
Initial orthonormal basis:

Deformed orthonormal basis:

We assume that these coincide.
Motion


Effect of  :
:

Dyadic notation:

Index notation:

The determinant of the deformation gradient is usually denoted by  and is a measure of the change in volume, i.e.,
and is a measure of the change in volume, i.e.,

Push Forward and Pull Back
Forward Map:

Forward deformation gradient:

Dyadic notation:

Effect of deformation gradient:
![{\displaystyle d\mathbf {x} ={\boldsymbol {F}}\bullet d\mathbf {X} ={\boldsymbol {\varphi }}_{*}[d\mathbf {X} ]}](../713a1b1c9ed4308419a4ab4f71798cd1ce9d85c6.svg)
Push Forward operation:
![{\displaystyle {\boldsymbol {\varphi }}_{*}[\bullet ]}](../abf24ff735450b28309aac3d548750c794487a62.svg)
 = material vector.
= material vector. = spatial vector.
= spatial vector.
Inverse map:

Inverse deformation gradient:

Dyadic notation:

Effect of inverse deformation gradient:
![{\displaystyle d\mathbf {X} ={\boldsymbol {F}}^{-1}\bullet d\mathbf {x} ={\boldsymbol {\varphi }}^{*}[d\mathbf {x} ]}](../338931a885b45a4e2085dca70d44a4640270f165.svg)
Pull Back operation:
![{\displaystyle {\boldsymbol {\varphi }}^{*}[\bullet ]}](../eafa2b8d8f39890a595387e5b697cabc27cf8623.svg)
 = material vector.
= material vector. = spatial vector.
= spatial vector.
Example
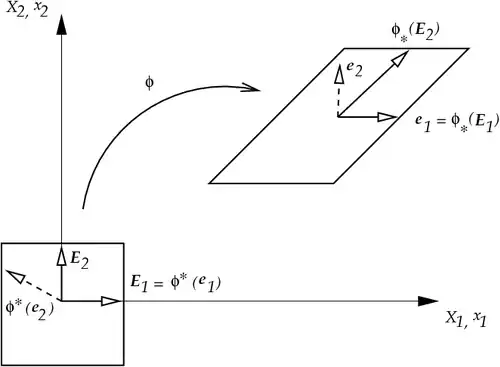 Push forward and pull back Push forward and pull back |
Motion:

Deformation Gradient:

Inverse Deformation Gradient:

Push Forward:
![{\displaystyle {\begin{aligned}{\boldsymbol {\varphi }}_{*}[{\boldsymbol {E}}_{1}]&=\mathbf {F} {\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}1\\0\end{bmatrix}}\\{\boldsymbol {\varphi }}_{*}[{\boldsymbol {E}}_{2}]&=\mathbf {F} {\begin{bmatrix}0\\1\end{bmatrix}}={\begin{bmatrix}1.5\\1.5\end{bmatrix}}\end{aligned}}}](../652db2dcb31ef3607763298cdab252d58a0be2a6.svg)
Pull Back:
![{\displaystyle {\begin{aligned}{\boldsymbol {\varphi }}^{*}[\mathbf {e} _{1}]&=\mathbf {F} ^{-1}{\begin{bmatrix}1\\0\end{bmatrix}}={\begin{bmatrix}1\\0\end{bmatrix}}\\{\boldsymbol {\varphi }}^{*}[\mathbf {e} _{2}]&=\mathbf {F} ^{-1}{\begin{bmatrix}0\\1\end{bmatrix}}={\begin{bmatrix}-1\\2/3\end{bmatrix}}\end{aligned}}}](../f07d9e3ad19c9b64b119f090c564767fe1ea7dd1.svg)
Recall:

Therefore,

Using index notation:

Right Cauchy-Green tensor:

Recall:

Therefore,

Using index notation:

Left Cauchy-Green (Finger) tensor:

Strain Measures
Green (Lagrangian) Strain

Green strain tensor:
![{\displaystyle {\begin{aligned}{\boldsymbol {E}}&={\frac {1}{2}}({\boldsymbol {C}}-{\boldsymbol {I}})\\&={\frac {1}{2}}({\boldsymbol {F}}^{T}\bullet {\boldsymbol {F}}-{\boldsymbol {I}})\\&={\frac {1}{2}}\left[{\boldsymbol {\nabla }}_{o}\mathbf {u} +({\boldsymbol {\nabla }}_{o}\mathbf {u} )^{T}+{\boldsymbol {\nabla }}_{o}\mathbf {u} \bullet ({\boldsymbol {\nabla _{o}\mathbf {u} )^{T}}}\right]\end{aligned}}}](../e2d8cf60e20678a55257c8ad49406f81d80b786d.svg)
Index notation:

Almansi (Eulerian) Strain

Almansi strain tensor:

Index notation:

Push Forward and Pull Back
Recall:

Now,

Therefore,

Push Forward:
![{\displaystyle \mathbf {e} ={\boldsymbol {\varphi }}_{*}[{\boldsymbol {E}}]={\boldsymbol {F}}^{-T}\bullet {\boldsymbol {E}}\bullet {\boldsymbol {F}}^{-1}}](../343ab8184fc12658afc4dd85752b5b107f10e0ab.svg)
Pull Back:
![{\displaystyle {\boldsymbol {E}}={\boldsymbol {\varphi }}^{*}[\mathbf {e} ]={\boldsymbol {F}}^{T}\bullet \mathbf {e} \bullet {\boldsymbol {F}}}](../dc21be32672cb75ab1991dfca79c183ee6ecda0e.svg)
Some useful results
The derivative of J with respect to the right Cauchy-Green deformation tensor ( ) is also often encountered in continuum mechanics.
) is also often encountered in continuum mechanics.
To calculate the derivative of  with respect to
with respect to  , we recall that (for any second order tensor
, we recall that (for any second order tensor  )
)

Also,
![{\displaystyle {\frac {\partial J}{\partial {\boldsymbol {F}}}}:{\boldsymbol {T}}={\frac {\partial J}{\partial {\boldsymbol {C}}}}:({\frac {\partial {\boldsymbol {C}}}{\partial {\boldsymbol {F}}}}:{\boldsymbol {T}})={\frac {\partial J}{\partial {\boldsymbol {C}}}}:({\boldsymbol {T}}^{T}\cdot {\boldsymbol {F}}+{\boldsymbol {F}}^{T}\cdot {\boldsymbol {T}})=\left[{\boldsymbol {F}}\cdot {\frac {\partial J}{\partial {\boldsymbol {C}}}}\right]:{\boldsymbol {T}}+\left[{\boldsymbol {F}}\cdot \left({\frac {\partial J}{\partial {\boldsymbol {C}}}}\right)^{T}\right]:{\boldsymbol {T}}}](../1729186785d49848ea9d533ddd8ed2ea4a59fc5e.svg)
From the symmetry of  we have
we have

Therefore, involving the arbitrariness of  , we have
, we have

Hence,

Also recall that

Therefore,

|
In index notation,

|
Derivative of the inverse of the right Cauchy-Green tensor
Another result that is often useful is that for the derivative of the inverse of the right Cauchy-Green tensor ( ).
).
Recall that, for a second order tensor  ,
,

In index notation

or,

Using this formula and noting that since  is a symmetric second order tensor, the derivative of its inverse is a symmetric fourth order tensor we have
is a symmetric second order tensor, the derivative of its inverse is a symmetric fourth order tensor we have

|

