hexaoctagonal tiling
Hexaoctagonal tiling
Poincaré disk model of the hyperbolic plane
TypeHyperbolic uniform tiling
Vertex configuration(6.8)2
Schläfli symbolr{8,6} or
Wythoff symbol2 | 8 6
Coxeter diagram
Symmetry group[8,6], (*862)
DualOrder-8-6 quasiregular rhombic tiling
PropertiesVertex-transitive edge-transitive

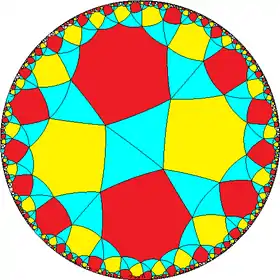
In geometry, the hexaoctagonal tiling is a uniform tiling of the hyperbolic plane.

Constructions

There are four uniform constructions of this tiling, three of them as constructed by mirror removal from the [8,6] kaleidoscope. Removing the mirror between the order 2 and 4 points, [8,6,1+], gives [(8,8,3)], (*883). Removing the mirror between the order 2 and 8 points, [1+,8,6], gives [(4,6,6)], (*664). Removing two mirrors as [8,1+,6,1+], leaves remaining mirrors (*4343).

Four uniform constructions of 6.8.6.8
Uniform
Coloring
Symmetry [8,6]
(*862)
 [(8,3,8)] = [8,6,1+]
(*883)
 [(6,4,6)] = [1+,8,6]
(*664)
 [1+,8,6,1+]
(*4343)
Symbol r{8,6} r{(8,3,8)} r{(6,4,6)}
Coxeter
diagram		 = = =

Symmetry

The dual tiling has face configuration V6.8.6.8, and represents the fundamental domains of a quadrilateral kaleidoscope, orbifold (*4343), shown here. Adding a 2-fold gyration point at the center of each rhombi defines a (2*43) orbifold. These are subsymmetries of [8,6].


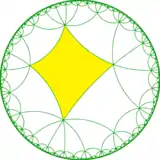[1+,8,4,1+], (*4343)
[(8,4,2+)], (2*43)
Uniform octagonal/hexagonal tilings
Symmetry: [8,6], (*862)
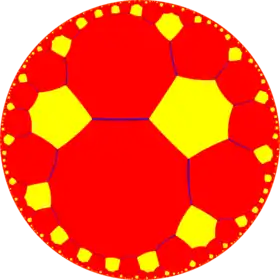
{8,6} t{8,6}
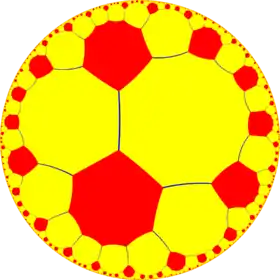
 r{8,6} 2t{8,6}=t{6,8} 2r{8,6}={6,8} rr{8,6} tr{8,6}
Uniform duals
V86 V6.16.16 V(6.8)2 V8.12.12 V68 V4.6.4.8 V4.12.16
Alternations
[1+,8,6]
(*466)		 [8+,6]
(8*3)		 [8,1+,6]
(*4232)		 [8,6+]
(6*4)		 [8,6,1+]
(*883)		 [(8,6,2+)]
(2*43)		 [8,6]+
(862)
h{8,6} s{8,6} hr{8,6} s{6,8} h{6,8} hrr{8,6} sr{8,6}
Alternation duals
V(4.6)6 V3.3.8.3.8.3 V(3.4.4.4)2 V3.4.3.4.3.6 V(3.8)8 V3.45 V3.3.6.3.8
Symmetry mutation of quasiregular tilings: 6.n.6.n
Symmetry
*6n2
[n,6]		 Euclidean Compact hyperbolic Paracompact Noncompact
*632
[3,6]		 *642
[4,6]		 *652
[5,6]		 *662
[6,6]		 *762
[7,6]		 *862
[8,6]...		 *∞62
[∞,6]		  
[iπ/λ,6]
Quasiregular
figures
configuration
6.3.6.3
6.4.6.4
6.5.6.5
6.6.6.6
6.7.6.7
6.8.6.8
6.∞.6.∞
6.∞.6.∞
Dual figures
Rhombic
figures
configuration
V6.3.6.3
V6.4.6.4
V6.5.6.5
V6.6.6.6
V6.7.6.7
V6.8.6.8
V6.∞.6.∞
Dimensional family of quasiregular polyhedra and tilings: (8.n)2
Symmetry
*8n2
[n,8]		 Hyperbolic... Paracompact Noncompact
*832
[3,8]		 *842
[4,8]		 *852
[5,8]		 *862
[6,8]		 *872
[7,8]		 *882
[8,8]...		 *∞82
[∞,8]		  
[iπ/λ,8]
Coxeter
Quasiregular
figures
configuration
3.8.3.8
4.8.4.8
8.5.8.5
8.6.8.6
8.7.8.7
8.8.8.8
8.∞.8.∞		  
8.∞.8.∞

See also

Wikimedia Commons has media related to Uniform tiling 6-8-6-8.

References

  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.