The actual reason is that the operator $F_{\mu\nu}^{a}\tilde{F}^{\mu\nu,a}$ in general has non-zero matrix element
$$
\tag 1 \lim_{\mathbf p' \to \mathbf p}\langle N(\mathbf p')| F^{a}_{\mu\nu}\tilde{F}^{\mu\nu,a}|N(\mathbf p)\rangle = i\mu \bar{N}(\mathbf p)\gamma_{5}N(\mathbf p),
$$
where $N$ is the nucleon state and $\mu$ is dimensional constant. The same argument applies for the matrix element
$$
\tag 2 \lim_{\mathbf p' \to \mathbf p}\langle N(\mathbf p')|F^{a}_{\mu\nu}F^{\mu\nu,a}|N(\mathbf p) \rangle \simeq m_{N}\bar{N}(\mathbf p)N(\mathbf p),
$$
making actually one of main contributions in the nucleon mass.
Although $(1)$ looks reasonable, it is of course hard to evaluate it for getting the value of $\mu$, because it is non-perturbative. However, here can be used the chiral anomaly: any chiral transformation
$$
q_{f} \to e^{i\alpha_{f}\gamma_{5}}q_{f}, \quad f = u,d,s
$$
generates the shift $\theta \to \theta + 2\alpha_{f}$. Therefore it is possible to eliminate the $\theta$-term with appearing the phase in the quark mass matrix:
$$
M_{q} \to M_{q}\cdot \text{diag}\big(\text{exp}\left[2i\alpha_{u}\gamma_{5}\right],\text{exp}\left[2i\alpha_{d}\gamma_{5}\right],\text{exp}\left[2i\alpha_{s}\gamma_{5}\right]\big)
$$
It's then possible to realize that for small $\theta$ the phases matrix generates the shift
$$
\bar{q}M_{q}q \to \bar{q}M_{q}q + i\theta \frac{m_{u}m_{d}m_{s}}{m_{u}m_{d}+m_{d}m_{s}+m_{u}m_{s}}\bar{q}\gamma_{5}q,
$$
which effectively defines $\mu$ (up to numerical factor).
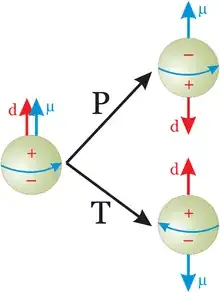
Once $(1)$ is derived, it's simple to obtain the dipole term. Classically, the dipole moment $d$ is defined through the hamiltonian
$$
H_{\text{EDM}} = d(\mathbf E \cdot \mathbf S),
$$
where $S$ is the spin operator and $\mathbf E$ is electric field. By using $(1)$, one realizes that one just needs to generate the operator
$$
L_{\text{EDM}} = d\cdot \bar{n}i\sigma_{\mu\nu}F^{\mu\nu}n
$$
This can be done only through the proton and pion fields, since the neutron doesn't have the tree-level coupling to photons. The latter is purely technical thing.